Einführung in die Geometrie ebener W-Kurven

von
Dieter Kötter

[aus : Christian Ostheimer / Renatus Ziegler : Skalen und Wegkurven , mit einem Beitrag von Dieter Kötter, Dornach 1996]
 
 

Inhalt    Textbeispiel: Weitere Sätze über W-Kurven. Anwendung auf die logarithmische Spirale

1. Projektive Abbildungen in der Ebene

2. Herleitung der Gleichungen der W-Kurven nach der Methode von Felix Klein

3. Allgemeine Eigenschaften der W-Kurven

Textbeispiel

3.2 Weitere Sätze über W-Kurven. Anwendung auf die logarithmische Spirale

Gegeben sei eine Gerade a, die eine W-Kurve K in O und O' schneidet. Die Tangenten in diesen Punkten an die Kurve seien t und t'. Wir beschränken uns zunächst auf den Fall, in dem t und t' noch mindestens einen weiteren Schnittpunkt P bzw. P' mit der Kurve K gemeinsam haben. Das ist bei den W-Kurven (Ia) mit Dornspitze und Wendepunkt und bei den Spiralen (Ib) der Fall. Dann gibt es in der Schar von Kollineationen, die K in sich überführen, genau eine, die O in O' und damit auch P in P' überführt. Wir verknüpfen sie mit der Kollineation, die O' auf P abbildet. Aus O wird dann P und aus O' der Punkt P', wenn wir die Reihenfolge der Kollineationen vertauschen. Dieselbe Kollineation ordnet also O, P ; O', P' ; O'', P'' usw. zu. Daraus folgt: Wenn die n Tangenten an eine W-Kurve in den n Schnittpunkten einer Geraden mit der Kurve weitere Punkte mit der W-Kurve gemeinsam haben, so liegen je n von ihnen wieder auf einer Geraden.

Da zwei beliebige solche Geraden a, a1, auf denen jeweils n Punkte liegen, projektiv zugeordnet sind, verbinden sowohl die Tangenten tn als auch die drei Fixgeraden entsprechende Punkte projektiver Punktreihen und hüllen einen Kegelschnitt ein, der auch a und a1 berührt. Wegen der Selbstdualität der W-Kurven läßt sich der duale Sachverhalt entsprechend beweisen.


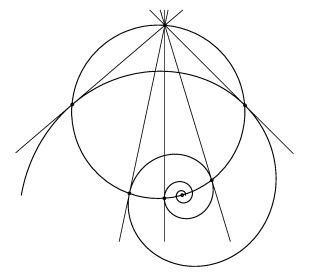
Abbildung 3.2 Berührpunktkreis einer logarithmischen Spirale.

Es gilt daher:

Satz 6
 
(a) Die Tangenten in den Schnittpunkten einer Geraden a mit einer W-Kurve hüllen einen Kegelschnitt ein, der die drei Fixgeraden und die Gerade a berührt. (b) Die Berührpunkte der Tangenten durch einen Punkt P an eine W-Kurve liegen auf einem Kegelschnitt, der durch die drei Fixpunkte und den Punkt P geht. 
 

Bei der logarithmischen Spirale ist der Kegelschnitt, wie man leicht einsehen kann, im Fall (a) eine Parabel. Da bezüglich der Parabel konjugierte Geraden durch den Brennpunkt sich rechtwinklig schneiden, berührt die Parabel die beiden imaginären Geraden i1 und i2 genau dann, wenn der Pol der Spirale der Brennpunkt der Parabel ist. Im Fall (b) ergibt sich unmittelbar, daß der Kegelschnitt ein Kreis durch den Pol U und den Punkt P sein muß (siehe Abbildung 3.2). Der Winkel über der Sehne UP ist dabei gleich dem konstanten Winkel zwischen Radius und Tangente (Peripheriewinkelsatz).

Sei K eine beliebige Kurve, die nicht zu einem W-Kurven-System gehört. Wenden wir auf K die Schar von Kollineationen des Systems an, so wird jede W-Kurve, die K berührt, in sich transformiert und berührt auch alle transformierten Kurven K. Es müssen daher die Einhüllenden dieser Kurven W-Kurven desselben Systems sein:

Satz 7

Wendet man auf eine beliebige Kurve K die Schar von Transformationen an, welche jede W-Kurve eines Systems in sich überführt, so entsteht eine Schar von Kurven K , deren Einhüllende W-Kurven desselben Systems sind.
Ein beliebiger Punkt der Kurve K wird auf die Punkte der W-Kurve abgebildet, die durch ihn geht.
Eine beliebige Tangente von K wird auf die Tangenten der W-Kurve abgebildet, die sie berührt.

Viele Eigenschaften der logarithmischen Spirale sind eine Folge dieses Satzes. Es sei S eine logarithmische Spirale eines Systems , t eine ihrer Tangenten sowie S' die an der Tangente gespiegelte Spirale (die nicht zum System gehört). Wendet man auf S' die Schar der Kollineationen an, so beschreibt der Pol von S' eine Spirale der Schar (siehe Abbildung 3.3). Mit anderen Worten:

die Zykloidale der logarithmischen Spirale ist eine logarithmische Spirale derselben Schar.


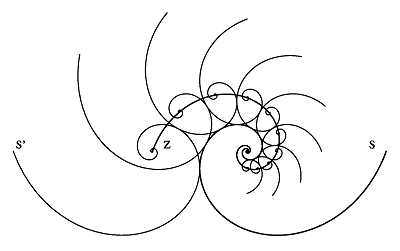
Abbildung 3.3 Die Zykloidale (Z) der logarithmischen Spirale (S).

Eine Gerade g bilde mit der Tangente t der Spirale S einen bestimmten Winkel, dem ein bestimmtes Doppelverhältnis entspricht. Wenden wir auf g die Schar von Transformationen an, so bleibt der Winkel zwischen g und t wegen der Konstanz des Doppelverhältnisses bei der Kollineation erhalten und die Einhüllende der Geradenschar g ist eine Spirale derselben Schar. Wie oben (Abschnitt 2.3) schon gezeigt, geht das Doppelverhältnis von vier Punkten in ein Verhältnis zweier Strecken über, wenn ein Punkt im Unendlichen liegt. Daraus folgt, daß bei den Kollineationen im Fall der logarithmischen Spirale nicht nur Winkel sondern auch Streckenverhältnisse erhalten bleiben. Wendet man die Kollineationen auf eine Normale oder auf eine Brennlinie der Spirale S an, so folgt dann mit Satz 7 unmittelbar:

Evolute, Antievolute, Kaustika, Perikaustika und Antikaustka einer logarithmischen Spirale sind Spiralen derselben Schar (Abbildung 3.3).

Den elementaren Beweis, daß die Antikaustika mit der Zykloidale zusammenfällt, übergehen wir hier.

Wir sehen nach dem Dargestellten, daß die besonderen Eigenschaften der logarithmischen Spirale, sich gewissermaßen immer wieder selbst zu erzeugen, nur euklidische Sonderfälle allgemeiner Eigenschaften der W-Kurven sind. Wenn BERNOULLI schrieb "Dem Maße nach unverändert und doch gewandelt wird sie auferstehen" (zit. nach BINDEL[1983]), so könnte man für eine W-Kurve sagen: dem projektiven Maße nach unverändert und doch gewandelt wird sie auferstehen.


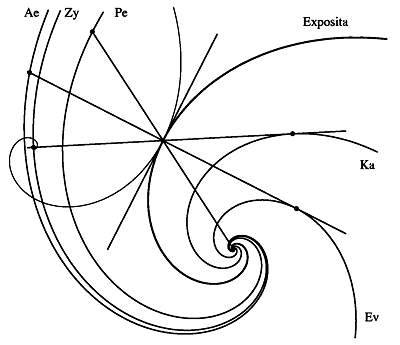
Abbildung 3.4 Evolute (Ev), Antievolute (Ae), Kaustika (Ka), Perikaustika (Pe) und Zykloidale (Zy) einer logarithmischen Spirale (Exposita).

Homepage Dieter Kötter

e-mail: d.koetter@t-online.de